题解 P5047

Description

给定一个长度为 $n$ 的序列 $\{a\}$ ，有 $q$ 次询问，每次询问区间 $[a,b]$ 的逆序对数。

Solution

二次离线莫队。先进行离散化。

我们可以预处理出对于一个位置 $a_i$，在他前面和后面分别有多少个数和它组成逆序对。

这可以用树状数组实现。

在莫队的过程中，更新区间可以利用记录的数组 $suf$ 和 $pre$ 来更新答案。

设原区间为 $[l,r]$，新区间 $[ql,qr]$。

那么更新ans就是 $suf_{ql}+pre_{qr}-(suf_l+pre_r)$ 。

但我们发现这样做会多算/少算，所以我们依次考虑每种情况。

1.1 ql<l

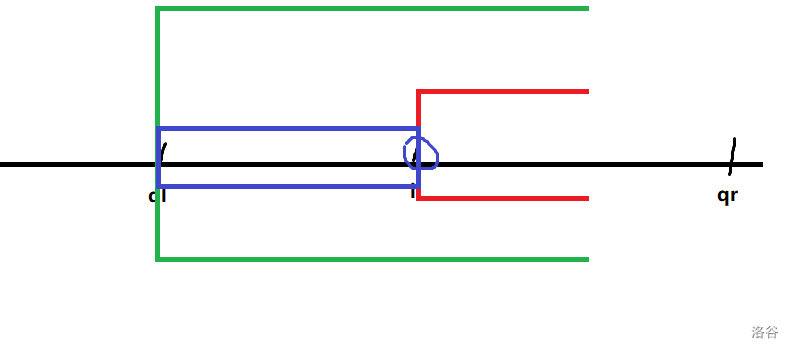
我们减去了红色的部分，加上了绿色的区域。

我们的意愿是除去 $[ql,l-1]$ 与当前区间的贡献。

显然，我们多考虑了 $[ql,l-1]$ 这个区间（蓝色）和qr之后的数组成逆序对的贡献。

把询问挂在qr+1的后缀询问上，询问它及它之后的数和这个区间的贡献。

权值设为 $-1$，因为要减去。

1.2 ql>l

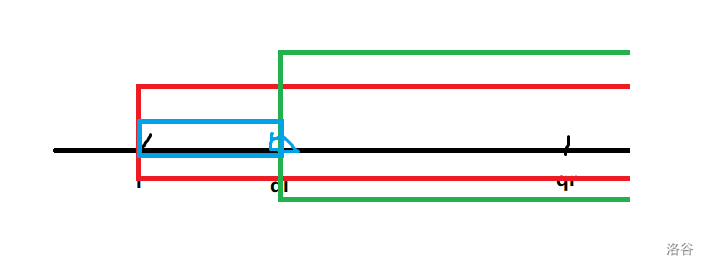
同理，这次是多减去了 $[l-1,ql]$ 的贡献。

那么在qr+1挂上它们和后面的数贡献的询问即可，权值为 $1$。

2.1 qr<r

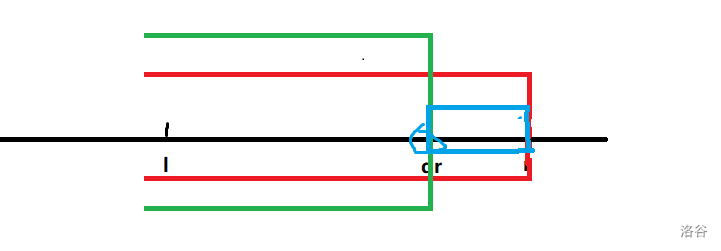
由于我们考虑的是前缀 $pre$，所以要计算它们和l之前的数的贡献。

注意：这里不是ql，而是l。

也就是我们需要计算的是和之前左端点的贡献。

为什么这样做呢：我们之前对l讨论的时候，已经把 $ql$ 和 $l$ 这两点之间的贡献消除了。

如若此时再和l相比，那么它们之间的贡献又会被考虑。

这一点明白了，剩下的就和上面一样了。

此时仍是不包含r这个点。询问挂在l-1上。

2.2 qr>r

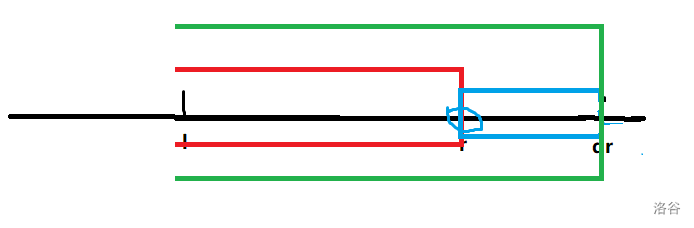
这和上面就一致了，多算了 $[r+1,qr]$ 的贡献。

在莫队过后，我们的答案与真正值只相差了挂在某些点的询问。

那么如何来统计这些询问呢？有个naive的想法仍旧是利用树状数组。

先算一算复杂度，询问的个数是 $O(m)$ 的。

挂起来的区间长度，每个询问是 $O(\sqrt n)$ 的，总共 $O(m\sqrt n)$。

树状数组单次操作 $O(\log n)$，显然是过不去的。

我们发现修改的操作比较少，询问比较多。

所以我们可以采用 $O(\sqrt n)$ 的时间修改，而要求 $O(1)$ 询问个数。

那么就可以值域分块了。

具体来说，可以维护每个数比它小/大的个数了。

新加入一个数时，在它前/后的值域加一。

整块直接加，零散块暴力。

查询时返回零散块和整块的和就可以了。

最后不要忘了乘上权值。

记得把答案累加，因为二次离线莫队算的是差值。

Code：

#include<bits/stdc++.h>
using namespace std;
namespace input
{
    const int InputBufferSize=(1<<23)+5;
    char buffer[InputBufferSize],*s,*eof;
    inline void init()
    {
        assert(stdin!=NULL);
        s=buffer;
        eof=s+fread(buffer,1,InputBufferSize,stdin);
    }
    inline bool read(int &x)
    {
        x=0;
        int flag=1;
        while(!isdigit(*s)&&*s!='-')s++;
        if(eof<=s)return false;
        if(*s=='-')flag=-1,s++;
        while(isdigit(*s))x=x*10+*s++-'0';
        x*=flag;
        return true;
    }
    inline bool read(char* str)
    {
        *str=0;
        while(isspace(*s))s++;
        if(eof<s)return false;
        while(!isspace(*s))*str=0,*str=*s,str++,s++;
        *str=0;
        return true;
    }
}
namespace output
{
    const int OutputBufferSize=(1<<23)+5;
    char buffer[OutputBufferSize];
    char *s=buffer;
    inline void flush()
    {
        assert(stdout!=NULL);
        fwrite(buffer,1,s-buffer,stdout);
        s=buffer;
        fflush(stdout);
    }
    inline void print(const char ch)
    {
        if(s-buffer>OutputBufferSize-2)flush();
        *s++=ch;
    }
    inline void print(char* str)
    {
        while(*str!=0)print(char(*str++));
    }
    inline void print(long long x)
    {
        char buf[25]= {0},*p=buf;
        if(x<0)print('-'),x=-x;
        if(x==0)print('0');
        while(x)*(++p)=x%10,x/=10;
        while(p!=buf)print(char(*(p--)+'0'));
    }
}
using namespace input;
using namespace output;
const int N=2e5+9;
#define ll long long
#define lowbit(x) (x&-x)
#define R register
int n,m,a[N],sum[N],maxn,len,block;
int bel[N];
ll tr[N],suf[N],pre[N],ans[N],Sum[N];

inline int get(int x){return x/len;}
struct Query
{
	int l,r,id;
	ll ans;
	bool operator < (const Query &a)const
	{
		return get(l)==get(a.l)?r<a.r:get(l)<get(a.l);	
	}
} Q[N];
struct query
{
	int l,r,id,t;
};

inline void add(int x,int c)
{
	while(x<=maxn)
	{
		tr[x]+=c;
		x+=lowbit(x);
	}
}

inline int ask(int x)
{
	int res=0;
	while(x)
	{
		res+=tr[x];
		x-=lowbit(x);
	}
	return res;
}

inline void add1(int x)
{//小于x的位置加一，分为整块Sum和零散块sum
	int pos=bel[x];
	for(int i=1;i<=bel[x]-1;i++) Sum[i]++;
	while(x>=1&&bel[x]==pos) sum[x]++,x--;
}

inline int query1(int x){return Sum[bel[x]]+sum[x];}

inline void add2(int x)
{//大于x的位置加一，分为整块Sum和零散块sum
	int pos=bel[x];
	for(int i=bel[x]+1;i<=bel[maxn];i++) Sum[i]++;
	while(x<=maxn&&bel[x]==pos) sum[x]++,x++;
}

inline int query2(int x){return Sum[bel[x]]+sum[x];}

vector<query> vecl[N],vecr[N];
vector<int> buk;
int main()
{
	init();read(n),read(m);
	len=sqrt(n);
	for(R int i=1;i<=n;i++) read(a[i]),buk.push_back(a[i]);
	sort(buk.begin(),buk.end());
	buk.erase(unique(buk.begin(),buk.end()),buk.end());
	for(R int i=1;i<=n;i++)
		a[i]=lower_bound(buk.begin(),buk.end(),a[i])-buk.begin()+1,maxn=max(maxn,a[i]);
	block=sqrt(maxn);
	for(R int i=0;i<=maxn;i++) bel[i]=i/block+1;
	for(int i=1;i<=n;i++) pre[i]=pre[i-1]+i-1-ask(a[i]),add(a[i],1);
	memset(tr,0,sizeof tr);
	for(int i=n;i>=1;i--) suf[i]=suf[i+1]+ask(a[i]-1),add(a[i],1);
	for(int i=1;i<=m;i++)
	{
		read(Q[i].l),read(Q[i].r);
		Q[i].id=i;
	}
	sort(Q+1,Q+1+m);
	int l=1,r=0;
	for(int i=1;i<=m;i++)
	{
		int ql=Q[i].l,qr=Q[i].r;
		Q[i].ans-=suf[l]+pre[r];
		Q[i].ans+=suf[ql]+pre[qr];//画图可知，两次区间多加/减了一些区域
		if(l>ql) vecr[qr+1].push_back({ql,l-1,i,-1});
		if(l<ql) vecr[qr+1].push_back({l,ql-1,i,1});
		if(r<qr) vecl[l-1].push_back({r+1,qr,i,-1});
		if(r>qr) vecl[l-1].push_back({qr+1,r,i,1});
		l=ql,r=qr;            
	}
	for(int i=1;i<=n;i++)
	{
		add1(a[i]);
		for(auto j:vecl[i])
		{
			int l=j.l,r=j.r,t=j.t,id=j.id;
			for(int k=l;k<=r;k++)//查询大于它的数,满足之前的数i下标小
				Q[id].ans+=1ll*t*query1(a[k]+1);
		}
	}
	memset(sum,0,sizeof sum);
	memset(Sum,0,sizeof Sum);
	for(int i=n;i>=1;i--)
	{
		add2(a[i]);
		for(auto j:vecr[i])
		{
			int l=j.l,r=j.r,t=j.t,id=j.id;
			for(int k=l;k<=r;k++)//查询小于它的数,满足之前的数i下标大
				Q[id].ans+=1ll*t*query2(a[k]-1);
		}
	}
	for(int i=2;i<=m;i++) Q[i].ans+=Q[i-1].ans;
	for(int i=1;i<=m;i++) ans[Q[i].id]=Q[i].ans;
	for(int i=1;i<=m;i++) print(ans[i]),print('\n');
	flush();
	return 0;
}