讲几棵平衡树
前置知识:BST。
...
1.Splay(伸展树)
Splay算是平衡树中比较重要的一种了,虽然不能可持久化,但仍有着举足轻重的地位。(文科生)
众所周知,Splay通过旋转,伸展来维持平衡。也是这个地方最难理解。(我就是这样)
先贴几张图
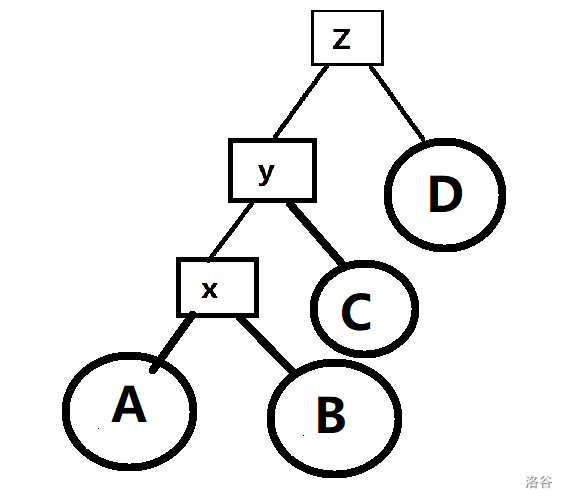
(画的巨丑的平衡树)
根据图我们知道tr[x].fa=y,tr[y]=z;
tr[x].ch[0]=A,tr[x].ch[1]=B
根据BST的性质,我们可以得到 A<x<B,x<y<c,y<z;
我们旋转,是要维护平衡树的树形结构,防止退化。所以我们应该把x旋转上去。
因为x<z,所以x是z的左孩子。
根据BST插入的性质,有x<B<y。
所以B被当作y的左儿子,C和A的相对位置不变。
把结论推广:x变为y原来的那个儿子,y变为x原来的相反儿子,其余儿子不变。
这样就旋转完成了!!!QWQ撒花★,°:.☆( ̄▽ ̄)$:.°★
你以为这就是splay吗,不,这只是splay的基操:rotate。
至于splay,还要更复杂一亿点点。
Tarjan曾说:Splay要靠双旋来维持平衡。
因为如果单旋的话,如上图,还是很容易被卡成链。(再两次rotate后z和y在一条链上)
这时候就要分情况讨论:
如果x,y,z,在一条链上,就要先旋y,再旋x;
这样就没有特别明显的链了(自行画图理解)
else,就旋两次x就行了。
另外注意细节:如果z点不存在(y就是根),要特判。
因为此时旋一次x就行了
(感谢yyb巨佬)
看代码吧(我懒得画图了)
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+9;
const int INF=1<<30;
struct Splay{
int ch[2];
int cnt,val,fa,siz;
} a[N];
inline void out()
{
cout<<"edwqedwq"<<endl;
}
int root,tot,n;
inline void update(int x)
{
a[x].siz=a[a[x].ch[0]].siz+a[a[x].ch[1]].siz+a[x].cnt;
}
inline void clear(int x)
{
a[x].fa=a[x].cnt=a[x].siz=a[x].val=a[x].ch[0]=a[x].ch[1]=0;
}
inline int ide(int p)
{
return a[a[p].fa].ch[1]==p;
}
inline void connect(int p,int fa,int son)
{
a[p].fa=fa,a[fa].ch[son]=p;
}
inline void rotate(int p)
{
int fa=a[p].fa,gfa=a[fa].fa,fson=ide(fa),son=ide(p);
connect(p,gfa,fson);
connect(a[p].ch[son^1],fa,son);
connect(fa,p,son^1);
update(fa),update(p);
}
inline void splay(int p)
{
for(int fa;(fa=a[p].fa);rotate(p))
{
if(a[fa].fa) rotate((ide(fa)==ide(p)?fa:p));
}
root=p;
}
inline void insert(int val)
{
int p=root,fa=0;
while(p&&a[p].val!=val) fa=p,p=a[p].ch[val>a[p].val];
if(p) a[p].cnt++,update(p);
else
{
p=++tot;
a[p].val=val;
a[p].fa=fa;
a[p].cnt=a[p].siz=1;
a[p].ch[0]=a[p].ch[1]=0;
if(fa) a[fa].ch[val>a[fa].val]=p;
}
splay(p);
}
inline void find(int val)
{
if(!root) return;
int p=root;
while(a[p].ch[val>a[p].val]&&a[p].val!=val) p=a[p].ch[val>a[p].val];
splay(p);
}
inline int get_rank(int p)
{
find(p);
return a[a[root].ch[0]].siz;
}
inline int pre()
{
int now=a[root].ch[0];
while(a[now].ch[1]) now=a[now].ch[1];
return now;
}
inline int nxt()
{
int now=a[root].ch[1];
while(a[now].ch[0]) now=a[now].ch[0];
return now;
}
inline void Delete(int p)
{
find(p);
if(a[root].cnt>1)
{
a[root].cnt--;
update(root);
return;
}//situation 1
if(!a[root].ch[0]&&!a[root].ch[1])
{
clear(root);
root=0;
return;
}
if(!a[root].ch[0])
{
int tem=root;
a[root=a[root].ch[1]].fa=0;
clear(tem);
return;
}
if(!a[root].ch[1])
{
int tem=root;
a[root=a[root].ch[0]].fa=0;
clear(tem);
return;
}
int tem=root,last=pre();
splay(last);
connect(a[tem].ch[1],root,1);
clear(tem);
update(root);
}
inline int get_val(int x)
{
x++;
int p=root;
while(1)
{
int ls=a[p].ch[0];
if(a[ls].siz>=x) p=ls;
else if(a[ls].siz+a[p].cnt<x)
{
x-=a[ls].siz+a[p].cnt;
p=a[p].ch[1];
}
else return a[p].val;
}
}
int main()
{
scanf("%d",&n);
insert(INF),insert(-INF);
int op,x;
while(n--)
{
scanf("%d%d",&op,&x);
switch(op)
{
case 1:
insert(x);
break;
case 2:
Delete(x);
break;
case 3:
printf("%d\n",get_rank(x));
break;
case 4:
printf("%d\n",get_val(x));
break;
case 5:
insert(x),printf("%d\n",a[pre()].val),Delete(x);
break;
case 6:
insert(x),printf("%d\n",a[nxt()].val),Delete(x);
break;
}
}
return 0;
}
2.Treap(传统树堆)
如果你理解了Splay的rotate操作,那么Treap便轻而易举。
Treap=Tree+Heap,也就是说,这是一种既满足BST,又符合堆的性质的数据结构。
BST由他的权值val体现,而堆则要靠我们随机赋的权dat体现。
堆是为BST服务的,如果子树过重,它的dat会很大,整棵树就不平衡了(这点和替罪羊很像)
这时我们就需要旋转来维护平衡,具体操作分为左旋和右旋
操作很简单,就把它和左(右)儿子换位就行,注意维护一下BST的性质。
(我曾经问过S1rius神仙:Treap会因为随机的dat被卡吗?)
如果你真的因为随机种子被卡了,而不是你写挂了,那么你可以去买彩票了。
贴一下代码(初学敲的李煜东的板子)
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+9;
const int INF=1<<30;
struct Treap{
int l,r;
int val,siz,cnt,dat;
} a[N];
int tot,root,n;
inline void update(int x)
{
a[x].siz=a[a[x].l].siz+a[a[x].r].siz+a[x].cnt;
}
inline int New(int val)
{
a[++tot].val=val;
a[tot].siz=a[tot].cnt=1;
a[tot].dat=rand();
return tot;
}
inline void build()
{
New(-INF),New(INF);
root=1,a[1].r=2;
update(1);
}
inline void zig(int &p)
{
int q=a[p].l;
a[p].l=a[q].r,a[q].r=p,p=q;
update(a[p].r),update(p);
}
inline void zag(int &p)
{
int q=a[p].r;
a[p].r=a[q].l,a[q].l=p,p=q;
update(a[p].l),update(p);
}
inline void insert(int &p,int val)
{
if(p==0)
{
p=New(val);
return;
}
if(val==a[p].val)
{
a[p].cnt++;
update(p);
return;
}
if(val>a[p].val)
{
insert(a[p].r,val);
if(a[a[p].r].dat>a[p].dat) zag(p);
}
else
{
insert(a[p].l,val);
if(a[a[p].l].dat>a[p].dat) zig(p);
}
update(p);
}
inline void Delete(int &p,int val)
{
if(p==0) return;
if(a[p].val==val)
{
if(a[p].cnt>1)
{
a[p].cnt--;
update(p);
return;
}
if(a[p].l||a[p].r)
{
if(a[p].r==0||a[a[p].l].dat>a[a[p].r].dat) zig(p),Delete(a[p].r,val);
else zag(p),Delete(a[p].l,val);
update(p);
}
else p=0;
return;
}
val<a[p].val?Delete(a[p].l,val):Delete(a[p].r,val);
update(p);
}
inline int get_rank(int p,int val)
{
if(p==0) return 0;
if(val==a[p].val) return a[a[p].l].siz+1;
if(val<a[p].val) return get_rank(a[p].l,val);
return get_rank(a[p].r,val)+a[p].cnt+a[a[p].l].siz;
}
inline int get_val(int p,int rank)
{
if(p==0) return INF;
if(a[a[p].l].siz>=rank) return get_val(a[p].l,rank);
if(a[a[p].l].siz+a[p].cnt>=rank) return a[p].val;
return get_val(a[p].r,rank-a[a[p].l].siz-a[p].cnt);
}
inline int get_pre(int val)
{
int p=root,pre;
while(p)
{
if(a[p].val<val) pre=a[p].val,p=a[p].r;
else p=a[p].l;
}
return pre;
}
inline int get_next(int val)
{
int p=root,nxt;
while(p)
{
if(a[p].val>val) nxt=a[p].val,p=a[p].l;
else p=a[p].r;
}
return nxt;
}
int main()
{
build();
scanf("%d",&n);
int op,x;
while(n--)
{
scanf("%d%d",&op,&x);
switch(op)
{
case 1:
insert(root,x);
break;
case 2:
Delete(root,x);
break;
case 3:
printf("%d\n",get_rank(root,x)-1);
break;
case 4:
printf("%d\n",get_val(root,x+1));
break;
case 5:
printf("%d\n",get_pre(x));
break;
case 6:
printf("%d\n",get_next(x));
break;
}
}
return 0;
}
3.fhq-Treap(非旋树堆)
不会,先咕着
4.Scapegoat Tree(替罪羊树)
咕
5.WBLT
去这里